| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- boj 2667
- 백준 1697
- boj 2470
- 백준 1503
- 백준 2636
- boj 2635
- boj 1697
- boj 1806
- 백준 2470
- boj 2167
- boj 1503
- 백준 1806
- boj 2206
- 백준 2167
- 백준 2178
- boj 2108
- boj 2661
- 백준 10800
- 10800
- 백준 2108
- boj 2636
- boj 19238
- boj 10800
- 백준 2635
- boj 2178
- 백준 2206
- 백준 2661
- 2636
- 백준 19238
- 2167
- Today
- Total
말랑말랑한 개발자 이야기
[코테를 위한 압축 개념] C++ STL 힙(Heap), 우선순위 큐(Priority queue) 본문
[코테를 위한 압축 개념] C++ STL 힙(Heap), 우선순위 큐(Priority queue)
Heap
Heap(힙)은 이진 트리 자료구조이다. 사진으로 보면 이해가 빠르다.

- index 0은 최상단 노드임을 의미한다.
- i 번째 노드의 자식 노드는 i * 2 + 1 번째 노드와 i * 2 + 2 번째 노드가 된다.
- i 번째 노드의 부모 노드는 (i - 1) / 2 번째 노드가 된다.
- 부모노드는 항상 자식 노드보다 작거나 같다. / 크거나 같다.
위 사진에서 트리 구조를 살펴보면 부모노드는 자식노드 보다 작은 규칙이 있다. 이러한 구조를 Min Heap이라고 한다. Heap은 두가지의 경우로 나뉘는데 위 사진과 반대로 부모가 자식보다 항상 큰 규칙을 가지면 Max Heap이 된다.
이러한 규칙을 유지하며 원소의 추가/제거 과정을 거치면 루트 노드에 있는 원소 값은 Min Heap에서는 최소값이, Max Heap에서는 최대값이 된다. 원소의 추가/제거하는 과정이 O(logN)의 복잡도를 갖고 조회는 O(1)으로 효율적인 구조이다.
push
위 트리 구조에 원소를 추가해보자. 예를 들어 4를 추가해보도록 하겠다.
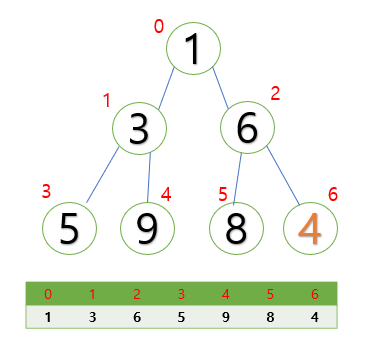
첫번째로 트리 구조의 제일 끝부분에 원소를 추가한다.
이 후 heap 규칙에 맞게 원소의 위치를 재설정할 필요가 있다. 4는 부모노드인 6보다 작기 때문에 위치를 서로 바꿔주어야 한다. 이러한 과정을 거치다보면 알맞은 위치를 찾을 수 있다.

pop

Heap에서 pop을 하게 되면 최상단 노드인 루트 노드가 구조에서 빠지게 된다.

이 후 제일 마지막 index에 해당 하는 노드가 그 빈 공간을 채운다.

push일 때는 말단에서 시작하여 부모노드와 비교를 했지만, pop의 경우에는 최상단 노드부터 시작해서 자식 노드와 비교해가며 알맞은 위치를 찾는다. 6의 자식노드는 3과 4이고 이 둘중 더 작은 값인 3이 6보다 작기 때문에 서로 위치를 바꾼다.

6의 자식노드는 5와 9이고 더 작은 값인 5는 6보다 작기 때문에 서로의 위치를 바꾼다. 따라서 위와 같은 구조를 최종적으로 갖는다.
구현하는 과정이 어렵지는 않으니 한 번 쯤은 직접 구현해보는것이 이해하는데 큰 도움이 된다.
Priority queue
위에서 본 Heap 자료구조롤 응용한 대표적인 사례가 Priority queue(우선순위 큐)이다. 우선순위 큐는 우선순위를 순차적으로 가져올 수 있는 push/ pop이 가능한 자료로 꼭 Heap으로 구현할 필요는 없지만 Heap으로 구현하는 것이 시간복잡도 면에서 큰 효율을 낼 수 있기 때문에 주로 Heap으로 구현한다. 따라서 이 두 개념이 같은 의미로 혼동되곤 하는데 개념적인 측면에서 이해하고 있을 필요가 있다.
Priority queue 비교
#include <iostream>
#include <queue>
using namespace std;
int main() {
queue<int> qu;
qu.push(1);
qu.push(9);
qu.push(5);
int sz = qu.size();
for(int i=0;i<sz;i++){
cout << qu.front() << ',';
qu.pop();
}cout << '\n';
priority_queue<int> p_qu_l;
p_qu_l.push(1);
p_qu_l.push(9);
p_qu_l.push(5);
sz = p_qu_l.size();
for(int i=0;i<sz;i++){
cout << p_qu_l.top() << ',';
p_qu_l.pop();
}cout << '\n';
priority_queue<int, vector<int>, greater<int>> p_qu_g;
p_qu_g.push(1);
p_qu_g.push(9);
p_qu_g.push(5);
sz = p_qu_g.size();
for(int i=0;i<sz;i++){
cout << p_qu_g.top() << ',';
p_qu_g.pop();
}cout << '\n';
return 0;
}일반 큐와 우선순위큐에 대한 비교이다. 우선순위 큐의 사용법은 일반 큐와 동일하지만 front 대신에 top을 쓴다는 차이점이 있다. 위 코드를 실행하면 아래의 결과를 얻을 수 있다.
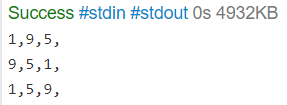
우선순위 큐는 기본적으로 Max Heap, 즉 원소를 pop하면 큰 수부터 내림차순으로 된다. 오름차순으로 하고 싶은 경우에는 원소에 전체적으로 음수를 취해주거나 우선순위 큐를 선언함에 있어 인자를 넣어 Min Heap을 만들어 주면 된다.
pair와 함께 사용하기
우선순위 큐는 알고리즘 문제를 푸는데 있어 활용도가 매우 높다. 특히 pair와 함께 사용되는 경우가 많은데 비교 우선순위는 pair의 첫번째 요소로 먼저 비교하고 같은 경우 그 두번째 요소로 비교하는 방식이다.
#include <iostream>
#include <queue>
using namespace std;
int main() {
priority_queue<pair<int,int>> temp;
temp.push(make_pair(3,100));
temp.push(make_pair(-2,140));
temp.push(make_pair(3,50));
temp.push(make_pair(49,12));
temp.push(make_pair(300,-20));
int sz = temp.size();
for(int i=0;i<sz;i++){
cout << temp.top().first << ',' << temp.top().second << '\n';
temp.pop();
}
return 0;
}위 코드를 실행하면 다음과 같은 결과를 볼 수 있다.

'알고리즘 > 개념' 카테고리의 다른 글
| [코테를 위한 압축 개념] C++ STL 맵(map), 셋(set) (0) | 2021.01.10 |
|---|---|
| [코테를 위한 압축 개념] C++ STL 벡터(vector), 큐(queue), 스택(stack), 덱(deque) (1) | 2021.01.04 |
